最优控制理论
Introduction
最优控制解决的是对某个给定的系统寻找其一个满足特定最优标准的控制规律。它是变分法的一个扩展,也是一种得到控制规律的数值最优方法。这一方法大部分由Lev Pontryagin和Richard Bellman发展,最优控制可以视为控制理论中的一个控制策略。一个控制问题包括一个损失泛函,它是状态变量与控制变量的函数。一个最优控制是描述最小化损失泛函控制变量路径的微分方程集合,它可以由Pontryagon极小法则(这是一个必要条件)得到,或者通过求解Hamilton-Jacobi-Bellman方程(充分条件)得到。
控制动力系统
令\(A\subset\mathbb{R}^m\),\(\mathbf{f} : \mathbb{R}^{n} \times A \rightarrow \mathbb{R}^{n}\),\(\alpha :[0, \infty) \rightarrow A\),考虑如下的动力系统: \[ \left\{\begin{array}{ll}{\dot{\mathbf{x}}(t)=\mathbf{f}(\mathbf{x}(t), \boldsymbol{\alpha}(t))} & {(t>0)} \\ {\mathbf{x}(0)=x^{0}}\end{array}\right.\tag{1.1} \] 我们称\(\boldsymbol{\alpha} :[0, \infty) \longrightarrow A\)为一个控制,对应每个控制的轨迹\(\mathbf{x}(\cdot)\)为对应系统的响应。
这里定义\(\mathcal{A}=\{\boldsymbol{\alpha} :[0, \infty) \rightarrow A | \boldsymbol{\alpha}(\cdot) \text {measurable }\}\)为可行控制空间。
损失泛函
通常来说损失泛函的形式如下: \[ P[\boldsymbol{\alpha}(\cdot)] :=\int_{0}^{T} r(\mathbf{x}(t), \boldsymbol{\alpha}(t)) d t+g(\mathbf{x}(T))\tag{1.2} \] 这里\(\mathrm{x}(\cdot)\)为\(\boldsymbol{\alpha}(\cdot)\)下动力系统的解,\(r : \mathbb{R}^{n} \times A \rightarrow \mathbb{R}\),\(g : \mathbb{R}^{n} \rightarrow \mathbb{R}\)为给定的度量。一般称\(r\)为控制代价,\(g\)为终止代价,终止点\(T>0\)也是提前给定的。
基本的问题是,我们想要在\(\mathcal{A}\)中找到一个能够最小化损失泛函的控制\(\alpha^{*}(\cdot)\),这引出了如下的三个问题:
- 最优控制的存在性
- 怎样刻画这个最优控制
- 最优控制如何构造
可控性与Bang-Bang 原理
仍然考虑式子\((1.1)\)描述的控制动力系统,我们从可控性问题开始。
可控性问题
给定初始点\(x^{0}\)以及一个目标集合\(S \subset \mathbb{R}^{n}\),是否存在一个控制能够在有限时间内将系统导引至\(S\)中?首先我们并不给定一个损失泛函以刻画某个最优控制,而是关注是否存在能够将系统导引至给定目标的控制,这里通常假定\(S=\{0\}\).
时刻t的可达集\(\mathcal{C}(t)\)为,由存在控制使得\(\mathbf{x}(t)=0\)的初值点\(x^{0}\)构成的集合。
全局可达集\(C\)为,存在控制及某个有限时间\(t\)使得\(\mathbf{x}(t)=0\)的初值点\(x^0\)构成的集合。
显然有如下关系成立: \[ \mathcal{C}=\bigcup_{t \geq 0} \mathcal{C}(t)\tag{2.1} \]
线性系统的可控性
很自然地,我们从最简单的一类控制系统开始: \[ \left\{\begin{array}{ll}{\dot{\mathbf{x}}(t)=M \mathbf{x}(t)+N \alpha(t)} & {(t>0)} \\ {\mathbf{x}(0)=x^{0}}\end{array}\right.\tag{2.2} \] 这里\(M \in \mathbb{M}^{n \times n}\),\(N \in \mathbb{M}^{n \times m}\),并限制控制参量的选取仅在一个单位方格中: \[ A=[-1,1]^{m}=\left\{a \in \mathbb{R}^{m}| | a_{i} | \leq 1, i=1, \ldots, m\right\}\tag{2.3} \] 我们可以得到系统\((2.2)\)的解析形式解: \[ \mathbf{x}(t)=\mathbf{X}(t) x^{0}+\mathbf{X}(t) \int_{0}^{t} \mathbf{X}^{-1}(s) N \alpha(s) d s\tag{2.4} \] 那么我们可以得到此时\(x^{0} \in \mathcal{C}(t)\)的等价条件: \[ x^{0}=-\int_{0}^{t} \mathbf{X}^{-1}(s) N \alpha(s) d s\tag{2.5} \] 若存在\(\alpha(\cdot) \in \mathcal{A}\)使得上式成立。
在线性控制系统中,可达集拥有比较好的性质:
- 可达集\(\mathcal{C}\)是对称(\(\pm x\)同时含于可达集中)且凸的
- 若\(x^{0} \in \mathcal{C}(\overline{t})\),则\(x^{0} \in \mathcal{C}(t)\)对任意\(t \geq \overline{t}\)成立
定义可控性矩阵为: \[ G=G(M, N) :=\underbrace{\left[N, M N, M^{2} N, \ldots, M^{n-1} N\right]}_{n \times(m n) \text { matrix }}\tag{2.6} \] 关于线性系统的可控性,有如下的等价条件: \[ \operatorname{rank} G=n\Leftrightarrow 0 \in \mathcal{C}^{\circ} \tag{2.7} \] 这里概括一下证明思路:1.若控制性矩阵的秩小于n,则零空间非空2.假设\(x^0\)在t时刻可达集中,利用等价条件\((2.5)\),可证零空间的元素必然正交于$x^0\(3.即\)C\(为控制性矩阵零空间的正交补空间,并且过原点,不存在内点4.相反若原点不是\)\(的内点,由其凸性可知在\)(t)$中有一个过\(0\)的支持平面,那么就可以找到其法向量,构造出一个控制性矩阵的非零解。
我们称线性系统可控若\(\mathcal{C}=\mathbb{R}^{n}\),有如下的定理:
令\(A\)为\(\mathbb{R}^n\)的单位立方体,假定控制性矩阵秩为\(n\),并且\(M\)的所有特征值实部为负,则系统是可控的。
实际上可以对条件进一步减弱,只要\(M\)的特征值实部非正即可,这里的证明比上面定理复杂很多。
Bang-Bang原理
这里仍然在单位立方体中选取控制,一个控制\(\alpha(\cdot) \in \mathcal{A}\)称为bang-bang若对于任意时刻都有\(\left|\alpha^{i}(t)\right|=1\)成立,可以理解为两状态控制。这是最为简单的一种控制,关于它有如下的定理:
若\(x^0\in \mathcal{C}(t)\),则对于线性控制系统\((2.2)\),存在一个bang-bang控制\(\alpha(\cdot)\)在t时刻将初值引导至原点。
关于它的证明,需要一些泛函分析的知识,这里先省略。
Pontryagin极小条件
变分法与哈密顿动力系统
给定一个光滑函数\(L : \mathbb{R}^{n} \times \mathbb{R}^{n} \rightarrow \mathbb{R}, L=L(x, v)\),\(L\)称为拉格朗日算子,这里\(T>0, x^{0}, x^{1} \in \mathbb{R}^{n}\)都是被给定的。
最开始的变分法考虑的是下面的优化问题: \[ I[\mathbf{x}(\cdot)] :=\int_{0}^{T} L(\mathbf{x}(t), \dot{\mathbf{x}}(t)) d t\tag{3.1} \] 这里\(\mathbf{x}(\cdot)\)满足\(\mathbf{x}(0)=x^{0}\)与\(\mathbf{x}(T)=x^{1}\),假定\(\mathbf{x}^{*}(\cdot)\)为\((3.1)\)的解,下面考虑如何刻画这个最优解。
欧拉-拉格朗日方程:若\(\mathbf{x}^{*}(\cdot)\)为变分问题\((3.1)\)的解,那么它满足以下的欧拉-拉格朗日微分方程: \[ \frac{d}{d t}\left[\nabla_{v} L\left(\mathbf{x}^{*}(t), \dot{\mathbf{x}}^{*}(t)\right)\right]=\nabla_{x} L\left(\mathbf{x}^{*}(t), \dot{\mathbf{x}}^{*}(t)\right)\tag{3.2} \] 这给出了一个必要条件,但如果我们能求解\((3.2)\),那么最优解就在这组解中。它的证明很容易查到,这里先省略。
下面我们将EL方程化简为一个一阶ODE,定义广义动量为: \[ \mathbf{p}(t) :=\nabla_{v} L(\mathbf{x}(t), \dot{\mathbf{x}}(t))\tag{3.3} \] 这里总假设我们能从式子\((3.3)\)反解出\(v\),定义一个动力系统的哈密顿子\(H : \mathbb{R}^{n} \times \mathbb{R}^{n} \rightarrow \mathbb{R}\)如下: \[ H(x, p)=p \cdot \mathbf{v}(x, p)-L(x, \mathbf{v}(x, p))\tag{3.4} \] 这里\(\mathbf{v}\)如上定义,有下面的定理:
若\(\mathbf{x}(\cdot)\)为EL方程的解,那么\((\mathbf{x}(\cdot), \mathbf{p}(\cdot))\)满足下面的哈密顿方程: \[ \left\{\begin{array}{l}{\dot{\mathbf{x}}(t)=\nabla_{p} H(\mathbf{x}(t), \mathbf{p}(t))} \\ {\dot{\mathbf{p}}(t)=-\nabla_{x} H(\mathbf{x}(t), \mathbf{p}(t))}\end{array}\right.\tag{3.5} \] 进一步,\(t \mapsto H(\mathbf{x}(t), \mathbf{p}(t))\)必然为常量映射,即满足极小性的、必然遵循某种守恒性。
拉格朗日乘子
如果定义域没有做任何限制,那么极值点的判别标准即梯度为零,下面考虑有限制的情况。
在\(R :=\{x \in \mathbb{R}^{n} | g(x) \leq 0\}\)中考虑,令\(x^{*} \in R\)并且有\(f(x^*)=\max _{x \in R} f(x)\),这里考虑如何刻画这个极值点。
若\(\mathrm{x}^*\)在\(R\)的内部,那么\(\nabla f\left(x^{*}\right)=0\).
若\(\mathrm{x}^*\)在\(\partial R\)上,考虑\(\nabla f\left(x^{*}\right)\)的方向。显然地,如下图所示的情况是不可能的:
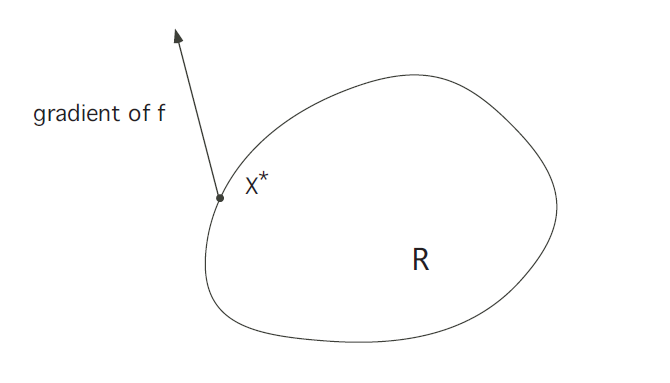
这表明\(\mathrm{x}^*\)在沿\(\partial R\)的方向上仍然存在非零的梯度,即并未达到极值,所以必然是下图所示的情况:
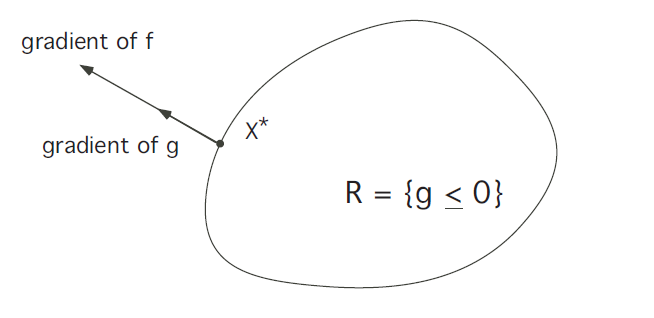
即\(\nabla f\left(x^{*}\right)\)必然与\(\partial R\)某处的法向量共线,这个法向量可以用\(\nabla g\left(x^{*}\right)\)表示,所以有下面的关系成立: \[ \nabla f\left(x^{*}\right)=\lambda \nabla g\left(x^{*}\right)\tag{3.6} \] 由于\(\nabla g\left(x^{*}\right)\)有可能为零,所以更加准确的描述如下:
存在不同时为零的实数\(\lambda\)与\(\mu\)使得: \[ \mu \nabla f\left(x^{*}\right)=\lambda \nabla g\left(x^{*}\right)\tag{3.7} \]
Pontyragin极小原理
核心的理论结果是,如果\(\alpha^{*}(\cdot)\)为一个最优控制,那么就对应着一个称为costate的函数\(\mathbf{p}^{*}(\cdot)\),它满足一个特定的极小性,我们应该把costate视作一类拉格朗日乘子。
定时自由终止点问题
控制理论哈密顿算子如下定义: \[ H(x, p, a) :=\mathbf{f}(x, a) \cdot p+r(x, a) \qquad\left(x, p \in \mathbb{R}^{n}, a \in A\right)\tag{3.8} \] 这里给出pontryagin极小原理的描述:
假定\(\alpha^{*}(\cdot)\)是满足\((1.1)\)与给定损失泛函下的最优控制,\(\mathrm{x}^{*}(\cdot)\)是对应的解,那么存在一个函数\(\mathrm{p}^{*} :[0, T] \rightarrow \mathbb{R}^{n}\),使得: \[ \begin{array}{c}{\dot{\mathbf{x}}^{*}(t)=\nabla_{p} H\left(\mathbf{x}^{*}(t), \mathbf{p}^{*}(t), \boldsymbol{\alpha}^{*}(t)\right)} \\ {\dot{\mathbf{p}}^{*}(t)=-\nabla_{x} H\left(\mathbf{x}^{*}(t), \mathbf{p}^{*}(t), \boldsymbol{\alpha}^{*}(t)\right)}\end{array}\tag{3.9} \] 并且此时: \[ H\left(\mathbf{x}^{*}(t), \mathbf{p}^{*}(t), \boldsymbol{\alpha}^{*}(t)\right)=\max _{a \in A} H\left(\mathbf{x}^{*}(t), \mathbf{p}^{*}(t), a\right) \qquad(0 \leq t \leq T)\tag{3.10} \] 进一步有\(t \mapsto H\left(\mathbf{x}^{*}(t), \mathbf{p}^{*}(t), \boldsymbol{\alpha}^{*}(t)\right)\)为常值映射,以及终止条件: \[ \mathbf{p}^{*}(T)=\nabla g\left(\mathbf{x}^{*}(T)\right)\tag{3.11} \] 这里\((3.9)\)的第二个式子是伴随方程,\((3.10)\)是极小(极大)原理。也称\((3.11)\)为截断条件,在之后会进一步讨论。
更加详细地,\((3.9)\)的第一个式子为: \[ \dot{x}^{i *}(t)=H_{p_{i}}\left(\mathbf{x}^{*}(t), \mathbf{p}^{*}(t), \boldsymbol{\alpha}^{*}(t)\right)=f^{i}\left(\mathbf{x}^{*}(t), \boldsymbol{\alpha}^{*}(t)\right)\tag{3.12} \] 这正是原始的控制系统方程。
伴随方程则为: \[ \begin{aligned} \dot{p}^{i *}(t) &=-H_{x_{i}}\left(\mathrm{x}^{*}(t), \mathbf{p}^{*}(t), \boldsymbol{\alpha}^{*}(t)\right) \\ &=-\sum_{j=1}^{n} p^{j *}(t) f_{x_{i}}^{j}\left(\mathrm{x}^{*}(t), \boldsymbol{\alpha}^{*}(t)\right)-r_{x_{i}}\left(\mathrm{x}^{*}(t), \alpha^{*}(t)\right) \end{aligned}\tag{3.13} \] 在深度学习中,大多都是定时自由终点问题,另一种情况(定终点自由时间问题)这里省略。
应用极小原理
对于控制问题,直接寻找一个最优控制\(\boldsymbol{\alpha}^{*}(\cdot)\)以及对应的解\(\mathrm{x}^{*}(\cdot)\)并不那么容易,我们可以通过求解\(\mathbf{p}^{*}(\cdot)\)来简化这个问题。这里以一个实际的例子来阐述这个过程:
构造一个简单的经济模型,以\(x(t)\)表示\(t\)时刻经济产量,\(\alpha(t)\)表示\(t\)时刻将产量再投资的比例,经济模型以如下的形式演化: \[ \left\{\begin{array}{l}{\dot{x}(t)=\alpha(t) x(t) \quad(0 \leq t \leq T)} \\ {x(0)=x^{0}}\end{array}\right.\tag{3.14} \] 我们希望极大化总消费量: \[ P[\alpha(\cdot)] :=\int_{0}^{T}(1-\alpha(t)) x(t) d t\tag{3.15} \] 使用pontryagin极小原理,有: \[ f(x, a)=x a, g \equiv 0, r(x, a)=(1-a) x\tag{3.16} \] 因此有: \[ H(x, p, a)=f(x, a) p+r(x, a)=p x a+(1-a) x=x+a x(p-1)\tag{3.17} \] 带入\((3.9)\)有: \[ \begin{array}\dot{x}(t)=H_{p}=\alpha(t) x(t)\\ \dot{p}(t)=-H_{x}=-1-\alpha(t)(p(t)-1)\end{array}\tag{3.18} \] 终止条件为: \[ p(T)=g_{x}(x(T))=0\tag{3.19} \] 最后,极大原理有: \[ H(x(t), p(t), \alpha(t))=\max _{0 \leq a \leq 1}\{x(t)+a x(t)(p(t)-1)\}\tag{3.20} \] 下面开始求解,根据\((3.20)\)有(\(x(t)>0\)): \[ \alpha(t)=\left\{\begin{array}{lll}{1} & {\text { if }} & {p(t)>1} \\ {0} & {\text { if }} & {p(t) \leq 1}\end{array}\right.\tag{3.21} \] 下一步需要确定\(p(\cdot)\),由\((3.18)\)及\((3.19)\)有: \[ \left\{\begin{array}{l}{\dot{p}(t)=-1-\alpha(t)[p(t)-1] \qquad(0 \leq t \leq T)} \\ {p(T)=0}\end{array}\right.\tag{3.22} \] 下面分情况讨论,若\(p(t)\le1\),则\(\alpha(t)=0\),因此\(\dot{p}(t)=-1\),那么有\(p(t)=T-t\),而这在满足假设的条件下成立,即\(T-1 \leq t \leq T\)时刻。
令一种情况,若\(p(t)>1\),则\(\alpha(t)=1\),有: \[ \dot{p}(t)=-1-(p(t)-1)=-p(t)\tag{3.23} \] 又由连续性,\(p(T-1)=1\),故而\(p(t)=e^{T-1-t}\),又需满足假设,可知这在\(0 \leq t \leq T-1\)上成立。
综上所述,最优控制为: \[ \alpha^{*}(t)=\left\{\begin{array}{ll}{1} & {\text { if } \quad 0 \leq t \leq t^{*}} \\ {0} & {\text { if } \quad t^{*} \leq t \leq T}\end{array}\right.\tag{3.24} \] \(t^{*}=T-1\).
动态规划
Bellman方程
考虑下面更一般的动力系统: \[ \left\{\begin{array}{l}{\dot{\mathbf{x}}(s)=\mathbf{f}(\mathbf{x}(s), \boldsymbol{\alpha}(s)) \quad(t \leq s \leq T)} \\ {\mathbf{x}(t)=x}\end{array}\right.\tag{4.1} \] 以及对应的损失泛函: \[ P_{x, t}[\boldsymbol{\alpha}(\cdot)]=\int_{t}^{T} r(\mathbf{x}(s), \boldsymbol{\alpha}(s)) d s+g(\mathbf{x}(T))\tag{4.2} \] 给定\(x \in \mathbb{R}^{n}, 0 \leq t \leq T\),定义价值函数\(v(x, t)\)为: \[ v(x, t) :=\sup _{\boldsymbol{\alpha}(\cdot) \in \mathcal{A}} P_{x, t}[\boldsymbol{\alpha}(\cdot)] \qquad\left(x \in \mathbb{R}^{n}, 0 \leq t \leq T\right)\tag{4.3} \] 价值函数给出了\(x,t\)的泛函.
Hamilton-Jacobi-Bellman方程刻画了价值函数,假定价值函数为\((x,t)\)的\(C^1\)函数,则\(v\)满足如下的方程: \[ \begin{array} vv_{t}(x, t)+\max _{a \in A}\left\{\mathbf{f}(x, a) \cdot \nabla_{x} v(x, t)+r(x, a)\right\}=0 \qquad\left(x \in \mathbb{R}^{n}, 0 \leq t<T\right)\\ v(x, T)=g(x) \qquad\left(x \in \mathbb{R}^{n}\right)\end{array}\tag{4.4} \] 我们可以将HJB写作: \[ v_{t}(x, t)+H\left(x, \nabla_{x} v\right)=0 \qquad\left(x \in \mathbb{R}^{n}, 0 \leq t<T\right)\tag{4.5} \] 这里的哈密顿子定义为: \[ H(x, p) :=\max _{a \in A} H(x, p, a)=\max _{a \in A}\{\mathbf{f}(x, a) \cdot p+r(x, a)\}\tag{4.6} \] 关于HJB方程的证明比较长,这里省略。
动态规划方法可以描述如下:
1.求解HJB方程,得到价值函数\(v\)
2.利用\(v\)来选取控制\(\boldsymbol{\alpha}(x, t)\),这里\(\boldsymbol{\alpha}(x, t)\)满足: \[ v_{t}(x, t)+\mathbf{f}(x, \boldsymbol{\alpha}(x, t)) \cdot \nabla_{x} v(x, t)+r(x, \boldsymbol{\alpha}(x, t))=0\tag{4.5} \] 3.求解如下的ODE,假定\(\boldsymbol{\alpha}(\cdot, t)\)拥有比较好的性质: \[ \left\{\begin{array}{ll}{\dot{\mathbf{x}}^{*}(s)=} & {\mathbf{f}\left(\mathbf{x}^{*}(s), \boldsymbol{\alpha}\left(\mathbf{x}^{*}(s), s\right)\right) \quad(t \leq s \leq T)} \\ {\mathbf{x}(t)=x}\end{array}\right.\tag{4.6} \] 4.定义反馈控制为: \[ \alpha^{*}(s) :=\alpha\left(\mathrm{x}^{*}(s), s\right)\tag{4.7} \] 总的来说,我们以这样的方式来设计最优控制:若系统的状态为\((x,t)\),我们使用在t时刻是的HJB的极小被满足的\(a \in A\).
可以证明,反馈控制即为一个最优控制,证明并不复杂。
由\((4.7)\)的定义以及式子\((4.5)\),有: \[ \begin{aligned} P_{x, t}\left[\boldsymbol{\alpha}^{*}(\cdot)\right] &=\int_{t}^{T}\left(-v_{t}\left(\mathbf{x}^{*}(s), s\right)-\mathbf{f}\left(\mathbf{x}^{*}(s), \boldsymbol{\alpha}^{*}(s)\right) \cdot \nabla_{x} v\left(\mathbf{x}^{*}(s), s\right)\right) d s+g\left(\mathbf{x}^{*}(T)\right) \\ &=-\int_{t}^{T} v_{t}\left(\mathbf{x}^{*}(s), s\right)+\nabla_{x} v\left(\mathbf{x}^{*}(s), s\right) \cdot \dot{\mathbf{x}}^{*}(s) d s+g\left(\mathbf{x}^{*}(T)\right) \\ &=-\int_{t}^{T} \frac{d}{d s} v\left(\mathbf{x}^{*}(s), s\right) d s+g\left(\mathbf{x}^{*}(T)\right) \\ &=-v\left(\mathbf{x}^{*}(T), T\right)+v\left(\mathbf{x}^{*}(t), t\right)+g\left(\mathbf{x}^{*}(T)\right) \\ &=-g\left(\mathbf{x}^{*}(T)\right)+v\left(\mathbf{x}^{*}(t), t\right)+g\left(\mathbf{x}^{*}(T)\right) \\ &=v(x, t)=\sup _{\boldsymbol{\alpha}(\cdot) \in \mathcal{A}} P_{x, t}[\boldsymbol{\alpha}(\cdot)] \end{aligned} \] 故而\(\boldsymbol{\alpha}^{*}(\cdot)\)是最优的.
我们以一个简单的例子来进一步阐述这个流程,
运输车以以下的方程运动, \[ \left(\begin{array}{c}{\dot{x}_{1}} \\ {\dot{x}_{2}}\end{array}\right)=\left(\begin{array}{ll}{0} & {1} \\ {0} & {0}\end{array}\right)\left(\begin{array}{c}{x_{1}} \\ {x_{2}}\end{array}\right)+\left(\begin{array}{c}{0} \\ {1}\end{array}\right) \alpha, \quad|\alpha| \leq 1 \] 损失泛函为, \[ P[\alpha(\cdot)]=-\text { time to reach }(0,0)=-\int_{0}^{\tau} 1 d t=-\tau \] 要使用动态规划,我们定义\(v(x_1,x_2)\)为负最小到达原点时间,起始点被定为\((x_1,x_2)\).
优于\(v\)并不依赖于\(t\),所以有: \[ \max _{a \in A}\left\{\mathbf{f} \cdot \nabla_{x} v+r\right\}=0 \] 并且, \[ A=[-1,1], \quad \mathrm{f}=\left(\begin{array}{c}{x_{2}} \\ {a}\end{array}\right), \quad r=-1 \] 那么有, \[ \max _{|a| \leq 1}\left\{x_{2} v_{x_{1}}+a v_{x_{2}}-1\right\}=0 \] 可得方程为: \[ \left\{\begin{array}{ll}{x_{2} v_{x_{1}}+\left|v_{x_{2}}\right|-1=0} & {\text { in } \mathbb{R}^{2}} \\ {v(0,0)=0}\end{array}\right. \] 下面检查方程是否满足,定义两个区域: \[ I :=\left\{\left(x_{1}, x_{2}\right)|x_{1} \geq-\frac{1}{2} x_{2}| x_{2} |\right\} \quad \text { and } \quad I I :=\left\{\left(x_{1}, x_{2}\right)|x_{1} \leq-\frac{1}{2} x_{2}| x_{2} |\right\} \] 直接计算得: \[ v(x)=\left\{\begin{array}{ll}{-x_{2}-2\left(x_{1}+\frac{1}{2} x_{2}^{2}\right)^{\frac{1}{2}}} & {\text { in Region I }} \\ {x_{2}-2\left(-x_{1}+\frac{1}{2} x_{2}^{2}\right)^{\frac{1}{2}}} & {\text { in Region II. }}\end{array}\right. \] 在区域\(I\)计算可得: \[ \begin{array}{l}{v_{x_{2}}=-1-\left(x_{1}+\frac{x_{2}^{2}}{2}\right)^{-\frac{1}{2}} x_{2}} \\ {v_{x_{1}}=-\left(x_{1}+\frac{x_{2}^{2}}{2}\right)^{-\frac{1}{2}}}\end{array} \] 因此: \[ x_{2} v_{x_{1}}+\left|v_{x_{2}}\right|-1=-x_{2}\left(x_{1}+\frac{x_{2}^{2}}{2}\right)^{-\frac{1}{2}}+\left[1+x_{2}\left(x_{1}+\frac{x_{2}^{2}}{2}\right)^{-\frac{1}{2}}\right]-1=0 \] 这表明了HJB在区域\(I\)是满足的,同样也可在区域\(II\)上得到验证。
由于\(\max _{|a| \leq 1}\left\{x_{2} v_{x_{1}}+a v_{x_{2}}+1\right\}=0\),所以可知最优控制为: \[ \alpha=\operatorname{sgn} v_{x_{2}} \]
动态规划与Pontryagin极小原理
特征方法
假定\(H : \mathbb{R}^{n} \times \mathbb{R}^{n} \rightarrow \mathbb{R}\)并考虑如下的Hamilton-Jacobi方程初值问题 \[ \left\{\begin{array}{l}{u_{t}(x, t)+H\left(x, \nabla_{x} u(x, t)\right)=0 \qquad\left(x \in \mathbb{R}^{n}, 0<t<T\right)} \\ {u(x, 0)=g(x)}\end{array}\right.\tag{4.8} \] 做以下的记号: \[ \mathbf{x}(t)=\left(\begin{array}{c}{x^{1}(t)} \\ {\vdots} \\ {x^{n}(t)}\end{array}\right), \mathbf{p}(t)=\nabla_{x} u(\mathbf{x}(t), t)=\left(\begin{array}{c}{p^{1}(t)} \\ {\vdots} \\ {p^{n}(t)}\end{array}\right)\tag{4.9} \] 下面引出特征方程,有: \[ p^{k}(t)=u_{x_{k}}(\mathbf{x}(t), t)\tag{4.10} \] 因此 \[ \dot{p}^{k}(t)=u_{x_{k} t}(\mathbf{x}(t), t)+\sum_{i=1}^{n} u_{x_{k} x_{i}}(\mathbf{x}(t), t) \cdot \dot{x}^{i}\tag{4.11} \] 假定\(u\)为式子\((4.8)\)的解,我们两边对\(x_k\)求导: \[ u_{t x_{k}}(x, t)=-H_{x_{k}}(x, \nabla u(x, t))-\sum_{i=1}^{n} H_{p_{i}}(x, \nabla u(x, t)) \cdot u_{x_{k} x_{i}}(x, t)\tag{4.12} \] 代入式子\((4.11)\)中: \[ \dot{p}^{k}(t)=-H_{x_{k}}(\mathbf{x}(t), \underbrace{\nabla_{x} u(\mathbf{x}(t), t)}_{\mathbf{p}(t)})+\sum_{i=1}^{n}(\dot{x}^{i}(t)-H_{p_{i}}(\mathbf{x}(t), \underbrace{\nabla_{x} u(x, t)}_{\mathbf{p}(t)}) u_{x_{k} x_{i}}(\mathbf{x}(t), t).\tag{4.13} \] 如果我们选取\(\mathbf{x}(\cdot)\)使得: \[ \dot{x}^{i}(t)=H_{p_{i}}(\mathrm{x}(t), \mathbf{p}(t)), \qquad(1 \leq i \leq n)\tag{4.14} \] 那么\((4.13)\)成为: \[ \dot{p}^{k}(t)=-H_{x_{k}}(\mathbf{x}(t), \mathbf{p}(t)), \qquad(1 \leq k \leq n)\tag{4.15} \] 这正是哈密顿方程: \[ \left\{\begin{array}{l}{\dot{\mathbf{x}}(t)=\nabla_{p} H(\mathbf{x}(t), \mathbf{p}(t))} \\ {\dot{\mathbf{p}}(t)=-\nabla_{x} H(\mathbf{x}(t), \mathbf{p}(t))}\end{array}\right.\tag{4.16} \] 接下来想要说明的是,如果我们能求解\((4.16)\),那么\((4.8)\)也被相应求解。 \[ \begin{aligned} \frac{d}{d t} u(\mathbf{x}(t), t) &=u_{t}(\mathbf{x}(t), t)+\nabla_{x} u(\mathbf{x}(t), t) \cdot \dot{\mathbf{x}}(t) \\ &=-H(\underbrace{\nabla_{x} u(\mathbf{x}(t), t)}_{\mathbf{p}(t)}, \mathbf{x}(t))+\underbrace{\nabla_{x} u(\mathbf{x}(t), t)}_{\mathbf{p}(t)} \cdot \nabla_{p} H(\mathbf{x}(t), \mathbf{p}(t)) \\ &=-H(\mathbf{x}(t), \mathbf{p}(t))+\mathbf{p}(t) \cdot \nabla_{p} H(\mathbf{x}(t), \mathbf{p}(t)) \end{aligned} \] 并且有\(u(\mathbf{x}(0), 0)=u\left(x^{0}, 0\right)=g\left(x^{0}\right)\),积分可得: \[ u(\mathbf{x}(t), t)=\int_{0}^{t}-H+\nabla_{p} H \cdot \mathbf{p} d s+g\left(x^{0}\right)\tag{4.17} \] 这即是\((4.8)\)的解,只要\(\mathbf{x}(\cdot)\)与\(\mathbf{p}(\cdot)\)被求解出来。
动态规划与Pontryagin极小原理的联系
回忆式子\((4.1)\)描述的更一般的动力系统,以及所定义的价值函数。这里主要的结果是,Pontryagin极小原理中的costate函数,实际上是价值函数\(v\)对\(x\)的梯度:
假定\(\alpha^{*}(\cdot), x^{*}(\cdot)\)为方程与损失泛函的最优控制和最优解,如果价值函数\(v\)为\(C^2\)的则极小原理中的costate\(\mathbf{p}^{*}(\cdot)\)满足以下的方程: \[ \mathbf{p}^{*}(s)=\nabla_{x} v\left(\mathbf{x}^{*}(s), s\right) \qquad(t \leq s \leq T)\tag{4.18} \] 其证明较长,这里省略。
微分博弈
定义
在深度学习中,博弈存在于GAN为代表的这类生成模型中,这在控制理论中也有对应的理论。这一节中讨论双人零和博弈(这正是GAN使用的)。基本的想法是,两个玩家分别控制两个动力系统,其中一个需要达到某种极大,另一个达到某种极小,并也存在着一个损失泛函。
对于两者最好的策略是什么?显然双方的行为不可能独立,任何一方的控制都会取决于另一方当前的状态。
我们对这个双控制的动力系统作出如下的定义:
给定\(0 \leq t<T\),以及两个集合\(A \subseteq \mathbb{R}^{m}\),\(B \subseteq \mathbb{R}^{l}\)与函数\(\mathrm{f} : \mathbb{R}^{n} \times A \times B \rightarrow \mathbb{R}^{n}\). 定义玩家一的控制为\(\boldsymbol{\alpha}(\cdot) :[t, T] \rightarrow A\),玩家二的控制为\(\boldsymbol{\beta}(\cdot) :[t, T] \rightarrow B\),最终的动力系统形式如下: \[ \left\{\begin{array}{l}{\dot{\mathbf{x}}(s)=\mathbf{f}(\mathbf{x}(s), \boldsymbol{\alpha}(s), \boldsymbol{\beta}(s)) \qquad(t \leq s \leq T)} \\ {\mathbf{x}(t)=x}\end{array}\right.\tag{5.1} \] 初始点\(x \in \mathbb{R}^{n}\)是被给定的。
博弈的损失泛函如下定义: \[ P_{x, t}[\boldsymbol{\alpha}(\cdot), \boldsymbol{\beta}(\cdot)] :=\int_{t}^{T} r(\mathbf{x}(s), \boldsymbol{\alpha}(s), \boldsymbol{\beta}(s)) d s+g(\mathbf{x}(T))\tag{5.2} \] 在博弈中,玩家一需要选取\(\alpha(\cdot)\)极大化\((5.2)\),玩家二则选取\(\boldsymbol{\beta}(\cdot)\)极小化\((5.2)\). 这就是我们所说的二人零和微分博弈,这里使用动态规划来研究这个问题。
映射\(\Phi : B(t) \rightarrow A(t)\)称为玩家一的策略若在任何\(t \leq s \leq T\)中, \[ \boldsymbol{\beta}(\tau) \equiv \hat{\boldsymbol{\beta}}(\tau) \quad \text { for } t \leq \tau \leq s\Rightarrow\Phi[\boldsymbol{\beta}](\tau) \equiv \Phi[\hat{\boldsymbol{\beta}}](\tau) \quad \text { for } t \leq \tau \leq s\tag{5.3} \] 我们可以认为\(\Phi[\boldsymbol{\beta}]\)是玩家一对玩家二所制定策略的响应,并且条件\((5.3)\)表明了玩家一并不能得到未来状态的信息。
玩家二的策略为映射\(\Psi : A(t) \rightarrow B(t)\),若对于任何\(t \leq s \leq T\), \[ \boldsymbol{\alpha}(\tau) \equiv \hat{\boldsymbol{\alpha}}(\tau) \quad \text { for } t \leq \tau \leq s\Rightarrow \Psi[\boldsymbol{\alpha}](\tau) \equiv \Psi[\hat{\boldsymbol{\alpha}}](\tau) \quad \text { for } t \leq \tau \leq s\tag{5.4} \] 并定义策略集合: \[ \begin{array}{l}{\mathcal{A}(t) :=\text { strategies for player } I \text { (starting at } t )} \\ {\mathcal{B}(t) :=\text { strategies for player } I I \text { (starting at } t )}\end{array} \] 接下来引入如下的价值函数,
下价值函数为: \[ v(x, t) :=\inf _{\Psi \in \mathcal{B}(t)} \sup _{\boldsymbol{\alpha}(\cdot) \in A(t)} P_{x, t}[\boldsymbol{\alpha}(\cdot), \Psi[\boldsymbol{\alpha}](\cdot)]\tag{5.5} \] 上价值函数为: \[ u(x, t) :=\sup _{\Phi \in \mathcal{A}(t)} \inf _{\boldsymbol{\beta}(\cdot) \in B(t)} P_{x, t}[\Phi[\boldsymbol{\beta}](\cdot), \boldsymbol{\beta}(\cdot)]\tag{5.6} \] 一个玩家宣布他的策略,即他对另一玩家策略的响应,然后由另一个玩家来选取控制。选取策略的玩家更有优势,即总有下面的关系成立: \[ v(x, t) \leq u(x, t)\tag{5.7} \]
动态规划与Isaacs方程
假定\(u,v\)都是\(C^1\)的,那么\(u\)满足上Isaacs方程: \[ \left\{\begin{array}{l}{u_{t}+\min _{b \in B} \max _{a \in A}\left\{\mathbf{f}(x, a, b) \cdot \nabla_{x} u(x, t)+r(x, a, b)\right\}=0} \\ {u(x, T)=g(x)}\end{array}\right.\tag{5.8} \] \(v\)满足下Isaacs方程: \[ \left\{\begin{array}{l}{v_{t}+\max _{a \in A} \min _{b \in B}\left\{\mathbf{f}(x, a, b) \cdot \nabla_{x} v(x, t)+r(x, a, b)\right\}=0} \\ {v(x, T)=g(x)}\end{array}\right.\tag{5.9} \] Isaacs方程实际上是HJB在双人零和博弈上的推广,同样我们可以对其进行如下改写: \[ u_{t}+H^{+}\left(x, \nabla_{x} u\right)=0\tag{5.10} \] 这里上哈密顿子定义为: \[ H^{+}(x, p) :=\min _{b \in B} \max _{a \in A}\{\mathbf{f}(x, a, b) \cdot p+r(x, a, b)\}\tag{5.11} \] 以及, \[ v_{t}+H^{-}\left(x, \nabla_{x} v\right)=0\tag{5.12} \]
\[ H^{-}(x, p) :=\max _{a \in A} \min _{b \in B}\{\mathbf{f}(x, a, b) \cdot p+r(x, a, b)\}\tag{5.13} \]
当博弈到达均衡时,就是我们所要求解的最优点,即有: \[ \max _{a \in A} \min _{b \in B}\{\mathbf{f}(\cdots) \cdot p+r(\cdots)\}=\min _{b \in B} \max _{a \in A}\{\mathbf{f}(\cdots) \cdot p+r(\cdots)\}\tag{5.14} \] 这时\(u\equiv v\),更加直接地,一个均衡状态可以如下描述: \[ P_{x, t}\left[\boldsymbol{\alpha}(\cdot), \boldsymbol{\beta}^{*}(\cdot)\right] \leq P_{x, t}\left[\boldsymbol{\alpha}^{*}(\cdot), \boldsymbol{\beta}^{*}(\cdot)\right] \leq P_{x, t}\left[\boldsymbol{\alpha}^{*}(\cdot), \boldsymbol{\beta}(\cdot)\right]\tag{5.15} \] 即双方任何一方进行控制的变动,都不会使得自己得到更好的结果。
Prontryagin极小原理与博弈
假定均衡条件\((5.14)\)满足,并且得到了最优的\(\alpha^{*}(\cdot), \beta^{*}(\cdot)\). 令\(\mathbf{x}^{*}(\cdot)\)为对应动力系统的解,定义: \[ \mathbf{p}^{*}(t) :=\nabla_{x} v\left(\mathbf{x}^{*}(t), t\right)=\nabla_{x} u\left(\mathbf{x}^{*}(t), t\right)\tag{5.16} \] 那么有以下的伴随方程: \[ \dot{\mathbf{p}}^{*}(t)=-\nabla_{x} H\left(\mathbf{x}^{*}(t), \mathbf{p}^{*}(t), \boldsymbol{\alpha}^{*}(t), \boldsymbol{\beta}^{*}(t)\right)\tag{5.17} \] 其中有博弈论哈密顿算子: \[ H(x, p, a, b) :=\mathbf{f}(x, a, b) \cdot p+r(x, a, b)\tag{5.18} \]